To calculate the required PFC capacitance we need to know the existing reactive power Q_L (VAR) of your electrical system and choose desired PF. The problem is Q_L is not always known. There are several ways of estimating Q_L, depending on what other quantities are known. We will discuss these methods below. It is important to point out the fact that reactive power of a motor is not constant and slightly varies with the load. Therefore, to avoid over correction, ideally you should determine VAR value of your motor at no-load. Unfortunately, the manufacturers rarely provide this number.

If you can't get Q_L information from the manufacturer, you can ask an electrician to measure idle current by using a clamp-on meter and multiply the result by the voltage. Technically, this will be total VA, but in absence of working power this result will be close to VAR. Once you determined "Q_L", the required rating of PFC capacitors will be simply Qc=Q_L×PF_desired, where PF is given as a decimal. If you are unable to determine no-load VAR, things get a bit more complicated. Let's recall from geometry that the tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side. Then, as we can see from power triangle diagram, uncorrected and corrected values of reactive power are given by the following equations:

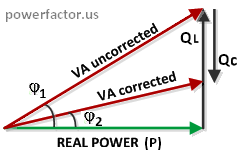Q_uncorrected=P×tanφ₁
Q_corrected=P×tanφ₂,
where P- real power. From this we find the required Qc:

Qc= Q_uncorrected-Q_corrected=P×(tanφ₁- tanφ₂)

We have three unknown values here: P, φ₁ and φ₂. Working power P can be measured by a wattmeter. To find φ₁ we need to know hypotenuse, which represents apparent power S(VA). So, you need to measure total current under full load and multiply it by the voltage. When we know P and S, assuming undistorted sinewave current without harmonics, we can find φ₁=arccos(P/S). Similarly, the desired angle φ₂ equals to φ₂=arccos(PF₂), where PF₂ is targeted power factor.

Finally, if measuring P and VA in your facility is unpractical, you have no choice but to collect HP, PF and efficiency numbers from your motor datasheet. This method is the least accurate one since the above data are provided for full load operation, while in reality the motors are almost always underloaded. Since 1hp≈0.746 kilowatt, if you don't know P, you can estimate it as
P(kW)=HP×0.746/η, where η is efficiency in decimal (typically 0.8 to 0.95). Substituting φ1 and φ2 into our expression for Qc we get:

Qc(kVAR)=P(kW)×[tan(arccos(PF₁))- tan(arccos(PF₂))],
where PF₁ and PF₂ are initial and improved PF respectively (if you have PF expressed in percentage, you need to divide it by 100). Our calculator just implements the above formula. Once you found required kVAR, select a standard capacitor with equal or smaller value. It is always better to under correct than over correct. Note that although normally capacitance is measured in microfarads, to simplify the sizing of PFC caps, manufacturers rate them in kilovars (kVAR). Since Ic=V/Xc and Xc=1/(2πFC), then V×I=2πFCV², where "C" is in farad, "F" is in hertz. If we express V×I in kVAR and "C" in μF, then the relationship between these two quantities is: kVAR=2πFC_μFV²×10^-9.





Our widget is for preliminary ballpark estimation only-- read our complete disclaimer linked below. You need an engineer to do a study, suggest a solution and determine if the project makes financial sense.